2021.3.15
逐次営農計画問題の解法プログラム
SP4XLP (Sequential Programming for XLP)
多段階計画モデルを利用して逐次営農計画問題の最適解を計算する機能を、線形計画法プログラムXLPに追加するExcelアドインです。
※ XLPはWindows版のバージョン2.47以降をご利用ください。
計算の手順
使い方
ダウンロード(解法プログラムと適用事例)
計算の手順
逐次営農計画問題の最適解は、次の手順で求めることができます。
1)多段階計画モデルを作成する。これは通常の線形計画モデルであるが、たとえば次のような手順で作成する。
(1)通常(単年度)の営農計画モデルを作成する。
(2)土地、労働、資本装備、資金等の経営資源について、前後の年度間の動態を表す制約式を導入する。これらを土地と資金で例示すれば、次のとおりである。以下、年度をt(1~T)で表す。
①自作地(t)=自作地(t-1)+耕地購入(t-1)
②経営耕地(t)=自作地(t)+耕地購入(t)+借地(t)
③期末預貯金(t)=期末預貯金(t-1)+借入金(t)-経営費(変動費)(t)-耕地購入費(t)-資本装備購入費(t)-生計費(t)+農産物販売収入(t)-支払利子(t)-元金償還金(t)
2)各年度(期間)の目標、たとえば農業所得額を表す年度目標(S.t)のプロセスを導入する。
年度目標(S.t)=農産物販売収入(t)-経営費(変動費)(t)-支払利子(t)-減価償却費(t)
3)年度目標(S.1)~年度目標(S.T)を目的関数とする計画問題(計画モデル)の最適解を順次求める。
①S.1を目的関数とする計画問題の最適解を求める。
②S.2を目的関数とする計画問題の最適解を求める。この際、「前年度(1年度)の年度目標の値は、前年度(1年度)の目標を目的関数とした計画問題の最適値以上である」という制約(年度目標の下限制約)を追加する。すなわち、最適解をS*.tとすれば、S.1≧S*.1 を追加する。この計画問題を解くと、前年度(1年度)の最適解が再現された上で、今年度(2年度)の最適解が求められる。
③3年度以降の最適解も、同様の手順で求める。すなわち、t年度の最適解を求める際には、S.t-1≧S*.t-1 を追加した計画問題の最適解を求める。
④これをT年度まで繰り返すことにより、(T-1)年度までの最適解が再現された上で、T年度の最適解が求められ、期間T年度の逐次計画問題の解が求められる。
4)なお、各年度目標の合計をZとし、
Z=S.1+S.2+・・・+S.T
とすれば、Zを目的関数とするモデルは多段階計画問題となり、その最適解は多段階計画問題の最適解となる。
使い方
計算の手順に示した処理を実行する"SP4XLP"の使い方は次のとおりです。
1)エクセルが動作している状態で、ファイル"sp4xlp.xla"を開く。すると、メニューバーの先頭にメニュー[XLP]が設置されます。それをクリックすると、サブメニュー一覧の一番下にサブメニュー[逐次計画]があります。
2)サブメニュー[逐次計画]を選ぶと、「年度目標_下限を入力すべきセル範囲」と「年度目標プロセスの利益係数を入力すべきセル範囲」を指定するフォームが開くので、2つのセル範囲を指定します(図1)。
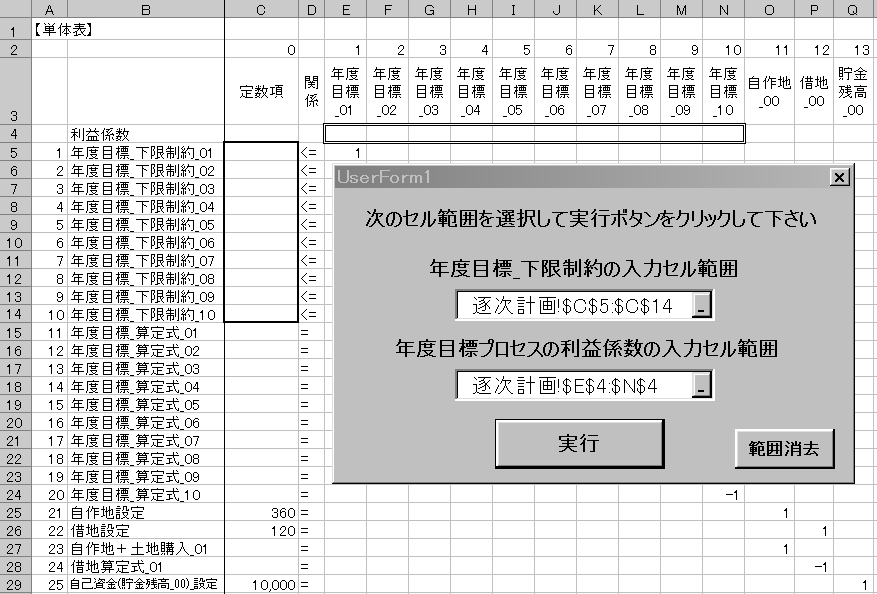
図1 セル範囲の指定
3)実行ボタンをクリックすると、順次、年度目標_下限(S*)が2)で指定したセルに記入されます(図2)。
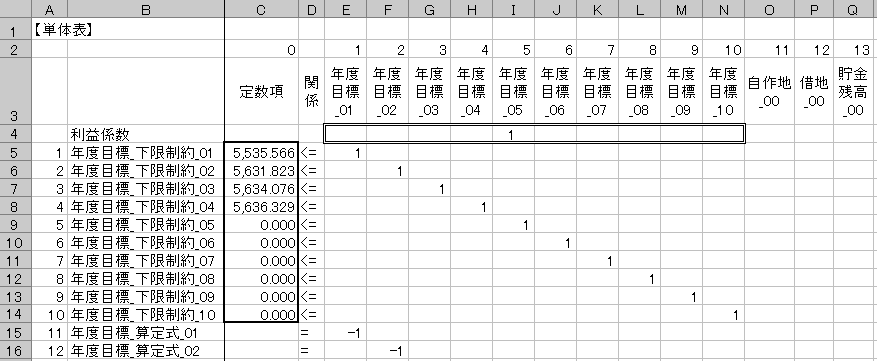
図2 処理画面(5年度の最適解の計算中)
4)最後に計算結果シートに逐次営農計画問題の解が表示されて、処理が終了します(図3)。
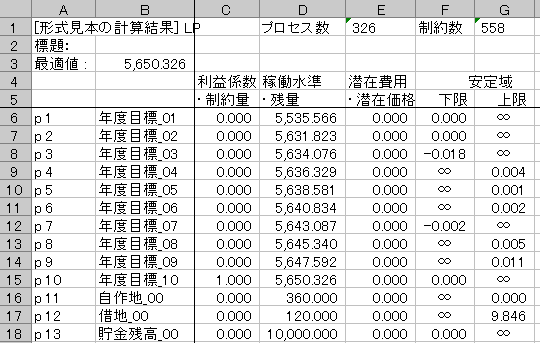
図3 終了画面(計算結果シート)
[以下、空白]



